[자료구조] 해시테이블(Hash Table) 정리 및 예제

해당 포스팅은 'Hello Coding 그림으로 개념을 이해하는 알고리즘' 도서를 개인공부하면서 정리한 내용입니다. 소스코드는 도서, 깃허브, 출판사 제공파일을 참고하였습니다. 깃허브 링크는 하단에 남겨두었습니다. 

| 해시 테이블이란?

해시 테이블은 해시함수와 배열 이용해 나타낸 자료구조 입니다. (1차원)배열은 배열 한 원소에 한 개의 값만 저장할 수 있지만, 해시 테이블의 배열은 한 배열에 여러 개의 원소를 저장할 수 있도록 연결리스트(linked list)를 이용합니다. 즉, 배열과 연결리스트로 구성된 복합 자료구조입니다. 

 

해시테이블 복합자료구조 모습

파이썬에서의 해시테이블 역할: 딕셔너리

파이썬에서 해시테이블은 딕셔너리로 표현할 수 있습니다. 딕셔너리는 키(key)와 값(value)로 구성된 자료구조 입니다. 이때 해시 함수를 사용하여 탐색에 시간복잡도 Big-O표기법으로 O(1)의 실행시간이 소요됩니다. 즉, 해시 함수를 이용해 데이터가 저장된 해시 테이블은 원하는 자료를 "바로" 탐색할 수 있습니다.

 

| 해시함수란?

해시함수는 문자열에 대한 숫자를 매핑(할당, mapping)하는 역할을 합니다. 즉, 문자열을 입력값으로 주면 숫자를 반환합니다. 

해시함수 특징

1.일관성

-첫번째 입력값이 melon이면 $0.5라는 가격을 반환합니다.  두번째 입력값이 mushroom이면 $0.5라는 가격을 반환합니다. 세번째에도 melon을 입력시 첫번째 때와 동일한 가격 $0.5를 반환하는 것이 일관성 있다는 것 입니다. 만약 $0.8을 반환하면 일관성이 없는 것 입니다. 

 

2.다른 입력값에는 다른 값이 나와야 합니다.

-정보보안에서 데이터가 변조가 되었을 경우 해시함수의 결과값이 달라지기 때문에 데이터의 무결성을 확인할 수 있습니다.

 

 

| 해시테이블과 해시함수의 관계

해시테이블은 저장할 수 있는 저장공간이고, 해시함수는 저장공간인 해시테이블에서 어디에 데이터를 저장할 지 결정하는 역할을 합니다. 해시함수에게 입력값을 주면 배열로 구성된 해시테이블에 저장할 위치인 배열 인덱스를 알려줍니다. 이 포스팅은 해시함수의 자세한 동작원리는 다루지 않습니다. 

 

 

| 해시테이블(딕셔너리) 구현방법-2

1. dict()

2. {}

#01_price_of_groceries.py
book = dict() # 해시테이블인 딕셔너리 생성
#[1] book = {"carrot":0.7, "milk":4, "avocado":3}
 
book["apple"] = True
book["melon"] = 10
book["tomato"] = 0.5
book = {"carrot":0.7, "milk":4, "avocado":3}
#book이 {}로 선언한 키/값으로 초기화 되어 apple, melon, tomato가 딕셔너리의 요소로 추가되지 않음
 
print(book)

 

주의사항

딕셔너리를 선언과 동시에 초기화하는 방법입니다. 위의 예시에서 딕셔너리 초기화가 맨 마지막에 이뤄졌습니다.

출력결과에서는 앞서 딕셔너리 값으로 추가한 apple, melon, tomato가 없습니다. 초기화로 인해 기존 정의한 내용이 없어진 것을 확인할 수 있습니다. 앞서 정의한 내용까지 출력하고 싶으면 초기화 부분을 맨 앞에 해야합니다.

book = {"carrot":0.7, "milk":4, "avocado":3}

출력결과

(1) book = {"carrot":0.7, "milk":4, "avocado":3}을 맨 뒤에만 적용_기존 내용 사라짐

(2) book = {"carrot":0.7, "milk":4, "avocado":3} 맨 처음에만 적용_ 기존 내용 존재

 

 

| 해시테이블

[1] 사용상황

1.조회

-전화번호, DNS

2.중복 방지

-투표

딕셔너리의 get()을 사용해서 get()의 매개변수로 key를 주면 value를 리턴받는다. 

voted = {}
def check_voter(person):
    #voted = {}
    if voted.get(person):
        print('이미 투표를 완료한 사람입니다.')
        return
    else:
        voted[person] = True
        print('아직 투표를 완료하지 않았습니다.투표하세요.')
        return
 
cnt = 0
while cnt<5:
    print("[{}] {}".format(cnt+1, "유권자 이름을 입력하세요: "), end='')
    person = input()
    check_voter(person)
    cnt += 1

 

해시테이블_중복 방지 

 

3.캐시

-서버는 사용자가 요청한 URL과 URL의 자료를 해시테이블로 구성하여 관리한다.

 

 

[2] 기능 

관계 표현

-정점(node)과 간선(edge)으로 구성된 그래프에서 두 정점(node)간 관계를 표현합니다.

-관계를 코드로 표현시 딕셔너리를 사용합니다. 

-너비우선탐색(BFS, Breadth-First-Search) 알고리즘에서 최단경로 문제 해결에서 그래프 1차 탐색범위(일촌), 2차 탐색범위(이촌)을 딕셔너리로 표현가능.

그래프 자료구조

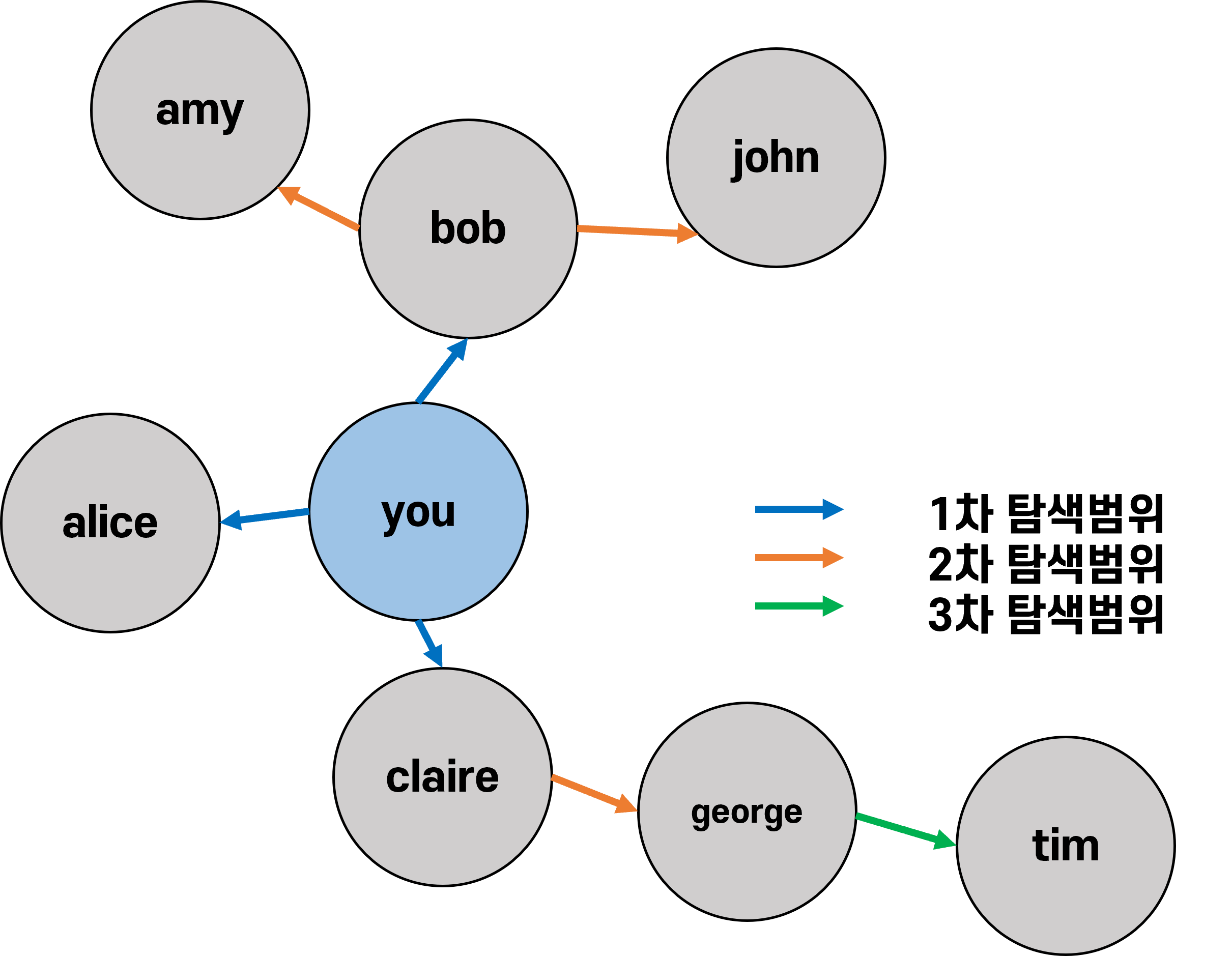
graph = {} #딕셔너리 생성
graph["you"] = ["alice", "bob", "claire"] #1차 탐색범위
graph["bob"] = ["amy", "john"] #2차 탐색범위
graph["alice"] = []
graph["claire"] =["george"]
graph["amy"] =[] #3차 탐색범위
graph["john"] =[]
graph["george"] = ["tim"]
graph["tim"] =[]# 4차 탐색범위

 

[3] 특징

순서 없음 

해시테이블은 키와 값으로 이뤄진 자료구조로 데이터 추가 시 순서를 유지하지 않습니다. 

 

 

[4] 성능 분석

해시테이블은 충돌(collision)이 발생하지 않아야 최악의 탐색, 삽입, 삭제 시간인 O(N)을 방지할 수 있습니다. 최악의 경우 탐색, 삽입, 삭제 시간이 O(N)이 소요됩니다. 

 

(1) 충돌(collision)이란?

충돌은 딕셔너리에서 두 개의 키(key)가 같은 공간에 할당된 상태를 말합니다. 이를 해결하기 위해 해시테이블은 배열이 연결리스트를 포함하게 되는 복합 자료구조 형태가 되었습니다. 즉, 한 배열 원소에 많은 연결리스트로 구성된 상태는 결국 연결리스트의 탐색시간 O(N)과 다를 바 없습니다. 한 원소의 연결리스트 크기가 커질 수록 해시테이블의 성능은 떨어집니다.

 

(2) 좋은 해시테이블의 요소

1.해시함수의 반환값의 분포가 고른 경우

-해시함수가 해시테이블에 데이터가 저장될 인덱스 반환시 분포를 넓게 시켜준다.

-연결리스트의 크기가 적다

-배열의 다양한 위치에 데이터가 분포되어있다.

2.낮은 사용률 

해시테이블은 배열로 구성되어 있기 때문에 저장공간이 거의 차거나 부족할 경우, 리사이징(resizing)을 통해 해시 테이블의 공간을 추가해야합니다. 리사이징의 기준은 사용률(load factor)로 파악합니다. 보통 사용률이 0.7보다 커지면 리사이징을 합니다.

해시테이블 성능분석_낮은 사용률_사용률 계산

 

해시테이블에 대해 정리를 마치겠습니다. 알고리즘은 처음 공부하는 단계입니다. 오류가 있으면 지적해주시면 감사하겠습니다.

| 참고도서

http://www.kyobobook.co.kr/product/detailViewKor.laf?mallGb=KOR&ejkGb=KOR&barcode=9788968483547

Hello Coding 알고리즘 - 교보문고

| 참고 소스코드

https://github.com/egonSchiele/grokking_algorithms/tree/master/05_hash_tables/python

GitHub - egonSchiele/grokking_algorithms: Code for the book Grokking Algorithms (https://amzn.to/29rVyHf)